
Understanding the Margin of Error in Surveys: Calculation, Interpretation, and Application
Margin of Error Calculator
Introduction to Margin of Error
In the realm of surveys and statistical analysis, understanding the concept of margin of error is paramount. It serves as a crucial indicator of the reliability and precision of survey results. In this article, we will delve into the definition of the margin of error, its relationship with confidence intervals, and its pivotal role in survey methodology—with a special focus on eCommerce brands and the surveys that are relevant to them.
Margin of error, often abbreviated as MOE, is a statistical measure used to quantify the uncertainty or potential variability in survey results. It represents the range within which the true population parameter is likely to fall, given a specific level of confidence.
An easy way to think of MOEs: If your survey has a 5% MOE, and the results were 47% “Yes”, then you can be sure that the percentage of the entire population that answered “Yes” is between 42-52%.
How the Margin of Error relates to Confidence Intervals
The margin of error is intimately connected to confidence intervals, which provide a range of values where the true population parameter is likely to exist. Typically expressed as a percentage, the confidence level dictates the width of the interval, and the margin of error is half of this interval's width. For instance, with a 95% confidence level, the margin of error is calculated such that we can be 95% confident that the true value lies within the range established by the survey.
The Role of Margin of Error in Surveys
Margin of error serves as a critical measure of the reliability and accuracy of survey results. A smaller margin of error implies higher precision and confidence in the findings, while a larger margin of error indicates greater uncertainty and potential variability.
Consider a political poll that shows Candidate A with 48% support and a margin of error of ±3%. This means there is a 95% chance that the true level of support for Candidate A falls between 45% and 51%. In other words, the margin of error provides a range within which the actual support for the candidate is likely to be.
For eCommerce surveys, if you’re polling your audience to choose between options A and B, the same concept of a margin of error applies, giving you a range within the support is likely to fall, without having to sample the whole population.
How to Calculate the Margin of Error
The margin of error is calculated using the following formula:
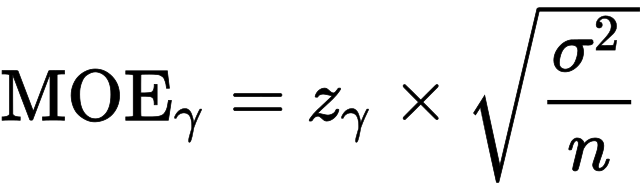
Where:
- MOE is the margin of error.
- z is the z-score corresponding to the chosen confidence level.
- σ is the population standard deviation.
- n is the sample size.
To calculate the margin of error, you need to follow these steps:
- Determine the desired confidence level (e.g., 95%, 99%).
- Find the appropriate z-score from a z-score table or calculator for the chosen confidence level.
- Collect data or estimate the population standard deviation (σ).
- Determine the sample size (n).
- Plug the values into the formula to compute the margin of error.
A z-score table provides the critical values required for calculating the margin of error at various confidence levels. The z-score corresponds to the level of confidence chosen for the survey and ensures that the margin of error is aligned with the desired level of precision. Here’s a z-score table with common confidence levels.
| Desired confidence level | z-score |
|---|---|
| 80% | 1.28 |
| 85% | 1.44 |
| 90% | 1.65 |
| 95% | 1.96 |
| 99% | 2.58 |
Let's consider a practical scenario where a ecommerce firm conducts a survey to estimate the average income of its customer base by polling them in a post-purchase survey.
Assuming a 95% confidence level, a population standard deviation of $10,000, and a sample size of 400, we can calculate the margin of error as follows:
MOE = 1.96 * (10,000 / √400) = $980
This means that with 95% confidence, the true average income in the city is likely to be within $980 of the estimated value obtained from the survey.
What confidence level should you choose when calculating your margin of error?
The choice of confidence level is a trade-off between precision and reliability. Higher confidence levels, such as 99%, result in wider intervals (larger margins of error) but provide greater confidence in the results. Lower confidence levels, like 90%, yield narrower intervals (smaller margins of error) but come with a lower level of confidence in the findings.
What sample size should you choose? How do sample size and margin of error values relate to each other?
Sample size plays a crucial role in determining the margin of error. As the sample size increases, the margin of error decreases, leading to more precise survey results. Conversely, smaller sample sizes result in larger margins of error and less precise estimates.
If a specific margin of error is required for a survey, researchers can adjust the sample size to achieve this goal. Increasing the sample size will decrease the margin of error, while decreasing the sample size will increase it.
It all boils down to this simple idea: the more data I have (sample size), the surer I can be about my guess (lower margin of error).
Conclusion
In conclusion, the margin of error is a critical concept in the world of surveys and statistical analysis. It quantifies the level of uncertainty in survey results and is closely tied to confidence intervals. By understanding the calculation of the margin of error and its relationship with sample size and confidence levels, researchers can design surveys that yield reliable and accurate data. In an era where data-driven decisions are essential, mastering the margin of error is a vital skill for anyone involved in survey research and analysis. It ensures that the insights obtained from surveys are not only insightful but also trustworthy.
Ready to know your customers better?
Book a demo








